Искусство и математика могут показаться двумя разными мирами, но они взаимосвязаны гораздо теснее, чем мы думаем. Многие художники показывали в своих работах великих математиков и их уникальные решения, которые потрясли весь мир. Мы решили показать такие шедевры, где геометрия точно оставила свой отпечаток в создании симметрии и баланса, иллюзии глубины и движения, которая завораживает взгляд и притягивает зрителя.

Почему мы испытываем наслаждение, глядя на шедевры
Искусство делает нас счастливыми так, как мы и не предполагали. Дело не только в эстетически приятных цветах или замысловатых деталях, но и в химических реакциях, происходящих в нашем мозге. Нейробиологи из Лондона обнаружили, что дофамин (нейромедиатор, связанный со счастьем и удовольствием) высвобождается, когда мы видим произведение искусства, которые нас восхищают. Это означает, что мозг настроен на то, чтобы испытывать радость и восторг при соприкосновении с таким произведением. От потрясающей картины до завораживающей скульптуры — искусство действительно способно поднять настроение и сделать нас более счастливым человеком.

«В живописи есть элемент баланса. Цвета, линии, темнота-свет, теплые-холодные тона… Это, конечно, своего рода математика. И математика, и искусство требуют много размышлений и много одиночества. Мне кажется, это самая глубокая связь между ними. И я не сомневаюсь, что хороший художник хорошо разбирается в математике. Когда я говорю, что он хорошо разбирается в математике, я имею в виду его математический образ мышления. Он может не знать математики, он может ее забыть, но это неважно», — считает турецкий математик Али Несин.
Задумчивый «Архимед» Доменико Фетти (1620 год)

Искусство математических открытий можно проследить до древнегреческого математика и изобретателя Архимеда. Благодаря своему острому уму и страсти к числам он заложил основы того, что стало одной из важнейших областей математики.
На картине Доменико Фетти «Архимед» 1620 года он изображен, погруженный в раздумья. Сложные детали его одеяния и тонкие тени, отбрасываемые фигурой, свидетельствуют о мастерстве художника. Но истинная уникальность произведения заключается в передаче эмоций. Можно почти почувствовать тяжесть мыслей Архимеда, размышляющего о тайнах мироздания. Неудивительно, что эта картина покоряет зрителей на протяжении многих веков, доказывая, что настоящее искусство способно преодолевать время и пространство.
«Смерть Архимеда» Томаса Деджорджа (1815 год)

Картина Томаса Дежоржа изображает мрачную сцену последних минут жизни математика. Сложная проработка деталей и мастерское использование света и тени притягивают зрителя, передавая эмоции момента.
«Ньютон» Уильяма Блейка (1795 год)

Замысловатая гравюра изображает знаменитого ученого, сидящего на скале в глубокой задумчивости и созерцании. Благодаря мускулистому телу и всклокоченным волосам интеллектуальный гигант выглядит почти богоподобным, что наводит на мысль о связи между знанием и силой. Поражает внимание Блейка к деталям — от тонких линий тела Ньютона до замысловатых узоров окружающего пейзажа.
«Портрет Луки Пачоли и неизвестного юноши» Якопо де Барбари (1500 год)

Лука Пачоли — знаменитый математик эпохи Возрождения. Пачоли в одеянии члена ордена францисканцев изображен за столом. Его левая рука опирается на раскрытую книгу, которая, как считается, является его Summa de Arithmetica, Geometria, Proportioni et Proportionalità или копией Евклида. Он чертит на доске с именем Евклида, окруженный инструментами математика: губкой, транспортиром, компасами, пером.
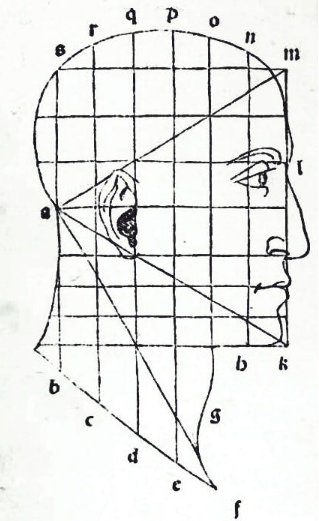
В правом углу стола изображен додекаэдр. В левой части картины изящно свисает ромбический кубооктаэдр. Личность молодого человека справа точно не установлена, но многие исследователи считают его «вечным студентом», которого наставлял Пачоли.
«Афинская школа» Рафаэля (1509 год)

В знаменитом шедевре Рафаэля группа величайших математиков мира собрана в одной яркой сцене. Мы видим всех — от Пифагора до Евклида. Картина представляет собой торжество не только искусства, но и красоты математики: все погружены в свои мысли и вычисления, а общая атмосфера располагает к интеллектуальному любопытству и исследованиям. Неудивительно, что эта картина стала одним из самых знаковых и любимых произведений искусства в мире, отражая самую суть встречи умов, которая происходит, когда искусство и математика соединяются в идеальной гармонии.
«Круги в круге», Василий Кандинский, 1923 г.

Кандинский был пионером абстрактного искусства и считал, что использование геометрических форм помогает создать ощущение гармонии и равновесия в его произведениях. В картине «Круги в круге» он использует круги разного размера и цвета для создания завораживающего эффекта. Круги словно пульсируют, увлекая зрителя вглубь произведения.
Отдельно стоит рассказать о Баухаусе — революционной художественной школе, которая привлекала наиболее новаторские умы начала XX века. Одним из них был Василий Кандинский, русский художник, чей смелый и экспрессивный стиль отразил суть модернистского движения.
Когда в 1922 году он поступил в Баухаус, то быстро завоевал популярность благодаря новаторской технике настенной живописи. Со временем его занятия стали одним из самых популярных. Своим преподаванием Кандинский вдохновил бесчисленное множество художников на исследование границ красок и создание авангардных и эмоционально сильных работ.
«Устный счет» Николая Богданова-Бельского (1895 год)

Картина запечатлела момент напряженной сосредоточенности и концентрации в учебном классе. Мальчики решают сложную математическую задачу. Использование теплых цветов и сложных деталей еще больше вовлекает зрителя в сцену.
«Небо и вода I» М.К. Эшера (1938 год)

М.К. Эшер известен своими завораживающими работами, которые изгибают реальность и бросают вызов разуму. Однако в его работах есть нечто большее, чем кажется на первый взгляд. При более глубоком рассмотрении его замысловатых иллюстраций обнаруживается математическая основа, которая помогла воплотить его проекты в жизнь.
Эшер был сильно вдохновлен паттернами и структурами, найденными в математике. Использование геометрических форм и тесселяций превратило его искусство в визуальное представление математических концепций. Возможно, именно поэтому многие считают Эшера одновременно и художником, и математиком.
Умелое манипулирование формами в гравюре «Небо и вода I» позволяет органично соединить два элемента, напоминая нам о том, что в природе все взаимосвязано. Именно благодаря художественной и математической гениальности Эшера мы можем его глазами увидеть сложность и гармонию окружающего нас мира.
«Звездная ночь» Ван Гога (1889 год)

Знаменитое произведение Винсента Ван Гога — воплощение фантазии художника. Переливы голубого и желтого цветов прекрасно передают блеск звездного неба в ясную ночь. Текстура и глубина картины переносят зрителя в безмятежное и спокойное место, где почти ощущается легкий ветерок в кипарисах.
Человеческий мозг обладает удивительной способностью распознавать и описывать закономерности, включая сложную концепцию турбулентного потока в гидродинамике. Хотя это явление по-прежнему трудно понять математически, искусство дало возможность визуализировать его проявления. Как раз ярким примером этого является картина Винсента Ван Гога, на которой с помощью круговых мазков кисти изображены клубящиеся облака и множество мерцающих звезд. Используя яркость, художники-импрессионисты уникальным образом изображали движение света, запечатлевая его перемещение по различным ландшафтам.
Физик Вернер Гейзенберг сказал: «Когда я встречусь с Богом, я задам ему два вопроса: почему относительность? И почему турбулентность? Я очень верю, что у него будет ответ на первый».
Однако исследователи, изучавшие работы Ван Гога, обнаружили скрытую в них отчетливую картину турбулентных структур жидкости, которая полностью совпадает с математическим уравнением, предложенным русским математиком Андреем Колмогоровым. Несмотря на внутренние переживания, Ван Гог сумел воспринять и изобразить одно из самых сложных явлений природы так, что оно до сих пор завораживает и вдохновляет зрителей.
«Номер 14» Джексона Поллока (1951 год)
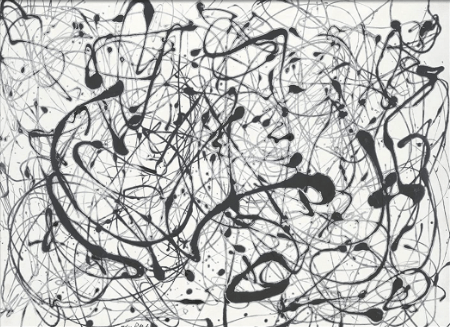
Творчество Джексона Поллока на протяжении многих лет восхищало как любителей искусства, так и математиков своим уникальным стилем. Его хаотичные и неограниченные картины позволили по-новому взглянуть на современное искусство, используя, казалось бы, случайные узоры и брызги, которые создают уникальный визуальный эффект.
Одни утверждают, что работы Поллока являются подлинными примерами фрактальной геометрии, другие спорят о том, может ли его искусство действительно воплощать это сложное математическое выражение. Как бы то ни было, творчество Поллока демонстрирует креативность и остается источником вдохновения для других.
«Витрувианский человек» Леонардо да Винчи (1490 год)
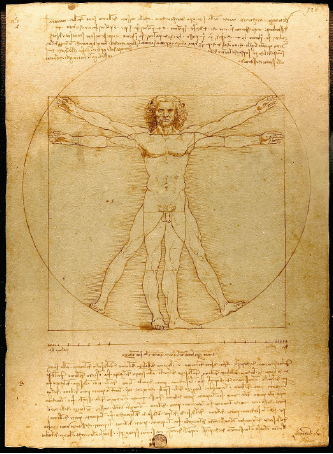
Произведение, в котором соблюден идеальный баланс между красотой и математической точностью. Невероятно детальный рисунок человеческой фигуры основан на точных измерениях и древних математических теориях из работ римского архитектора Витрувия.
«Мона Лиза» Леонардо да Винчи (1517 год)

Помимо загадочной улыбки и тайны, связанной с личностью женщины на портрете, это произведение искусства имеет и интересный математический аспект.

Леонардо да Винчи был человеком многих талантов, в том числе и математических. Широко распространено мнение, что при создании композиции картины художник использовал геометрию, применяя математическое золотое сечение для определения размеров и расположения каждого элемента. Действительно, «Мона Лиза» была детально проанализирована математиками, которые обнаружили множество геометрических закономерностей и связей.
Золотое сечение от архитектора Рафаэля Араужо

Золотое сечение — математическая закономерность, используемая в искусстве и архитектуре с древнейших времен. Явление всегда вызывает интерес как у художников, так и у математиков. Один из них — Рафаэль Араужо. Его замысловатые иллюстрации демонстрируют красоту золотого сечения и его проявление в мире природы. Уникальность творчества Араужо заключается в том, что он не использует компьютер для создания своих проектов. Вместо этого он прорисовывает каждую линию и изгиб вручную, что придает его работам ощущение органичной подлинности.
В следующий раз, когда будете любоваться каким-либо произведением искусства, обратите внимание на математическую точность, с которой оно было создано. Элегантность математики может оказаться той самой красотой, которая лежит в основе восприятия.
